Wzory matematyczne, których nie ma w karcie wzorów. 5 propozycji, które musisz znać!
O karcie wzorów, którą zapewnia każdemu maturzyście szkoła, wielokrotnie opowiadaliśmy już na blogu. Biegłe posługiwanie się kartą wzorów nie zagwarantuje Wam jednak pełnego sukcesu. Z racji, iż matura z matematyki zbliża się wielkimi krokami, warto do powtórek włączyć treści i wzory matematyczne, które znacznie usprawnią proces obliczeń. W poniższym wpisie zaproponujemy Wam aż 5 przydatnych wzorów, które nie pojawiają się w karcie wzorów.
Poznaj szybkie i przyjemne przygotowanie do matury 2025
Dołącz do naszej platformy, a my zamienimy Twoje powtórzenie do matury w grę! Wszystko czego potrzebujesz podane na tacy ✅
Wzór pierwszy – sześcian bez tajemnic
Sześcian to prostopadłościan zbudowany z sześciu jednakowych kwadratów. To cenna informacja, która pozwoli Ci w maturalnym stresie nie popełnić błędu. Jeśli oznaczymy bok sześcianu literką „a”, otrzymamy następujące wzory:
pole sześcianu → 6a2
objętość sześcianu → a3
przekątna sześcianu → a√3
przekątna ściany, czyli przekątna kwadratu → a√2
Wzory matematyczne przedstawione powyżej nie pojawiają się w w karcie wzorów, dlatego warto je zapamiętać, by w razie potrzeby móc w łatwy sposób obliczyć wymagane w zadaniu dane dotyczące sześcianu.
Wzór drugi – czyli o ułatwieniach w funkcji liniowej
Funkcja liniowa uznawana jest przez maturzystów za jedną z prostszych. Z tego też powodu zadania z nią w roli głównej zazwyczaj nie sprawiają im problemów. Warto jednak usprawnić sobie obliczenia i zapamiętać, że gdy wzór funkcji liniowej przedstawiony jest w postaci kierunkowej f(x) = ax+ b, możemy w prosty sposób wyliczyć współczynnik kierunkowy „a”.
Wystarczy, że podane będą dwa punkty, które należą do tej prostej, czyli A = (a,b) i B = (c,d). Wówczas możemy przy obliczeniach skorzystać z poniższego wzoru:
To również przykład na wzór matematyczny, którego nie ma w karcie wzorów. Nie da się ukryć, znacznie ułatwia on obliczenia w zakresie funkcji liniowej.
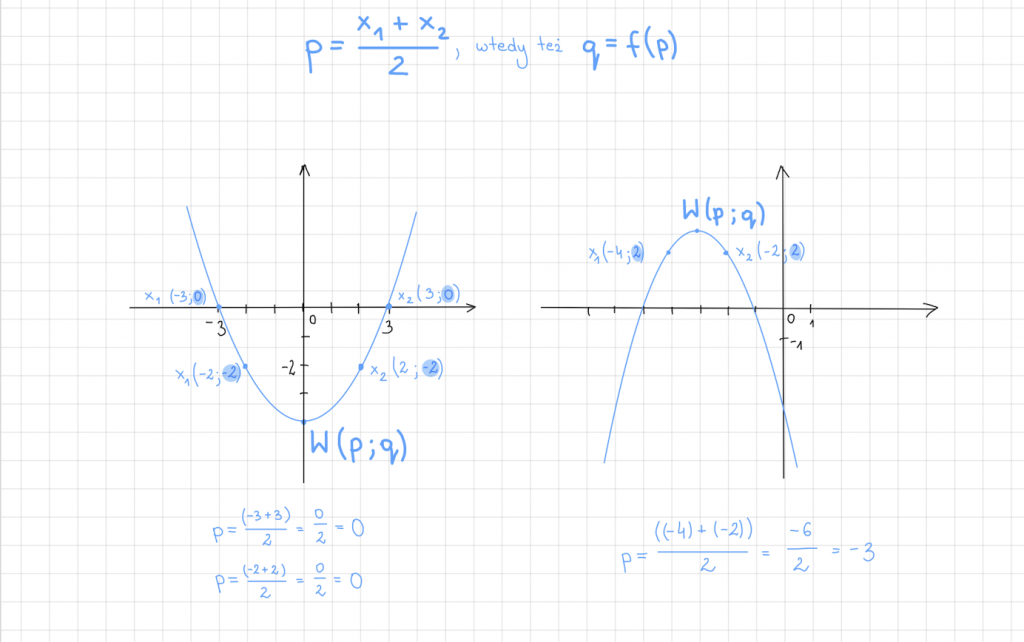
Wzór trzeci – wierzchołek funkcji kwadratowej
Wzory matematyczne mają to do siebie, że wymagają ciągłego powtarzania. Niestosowane w praktyce często ulatują z pamięci. Jest to szczególnie zauważalne podczas ważnych egzaminów, kiedy coś gdzieś dzwoni, ale nie wiadomo skąd i w jaki sposób…
Podobnie sprawy mają się w przypadku funkcji kwadratowej, co do której wprowadzono cały spis wzorów umożliwiających pozyskiwanie poszczególnych danych. Część z nich znajdziecie w karcie wzorów. Warto zapamiętać jednak sposób wyliczania współrzędnych wierzchołka paraboli. Można go obliczyć korzystając ze średniej arytmetycznej miejsc zerowych funkcji lub średniej arytmetycznej każdych dwóch argumentów, dla których funkcja przyjmuje te same wartości, czyli:
Wzór czwarty – o odcinkach w trapezie
Często zdarza się, że na maturze pojawia się zadanie z wykorzystaniem w trapezie odcinka łączącego środki ramion. Należy przede wszystkim zapamiętać, że odcinek ten jest w każdym trapezie równoległy do jego podstaw. W dodatku znajduje się idealnie pośrodku nich, dlatego można go obliczyć ze średniej arytmetycznej podstaw trapezu.
Wzór piąty– zależności w trójkątach prostokątnych o kątach 45, 45, 90 stopni oraz 30, 60, 90 stopni
Z trójkątami jest sporo zachodu, ale kiedy ogarnie się podstawy, bez trudu podoła się nawet bardziej wymagającym zadaniom. W wielu sytuacjach można znaleźć podpowiedzi w karcie wzorów, jednak na maturze często pojawiają się także pytania dotyczące trójkątów o specyficznych kątach, co do których należy przygotować się samodzielnie:
a) 45, 45 i 90 stopni
Powyższe miary świadczą o tym, że mamy do czynienia jednocześnie z trójkątem prostokątnym i równoramiennym. Aby bez trudu rozwiązywać zadania, w których ta figura się pojawia, warto zapamiętać, że długość przeciwprostokątnej w trójkącie o boku oznaczonym literą „a” można bez trudu obliczyć ze wzoru:
a√2
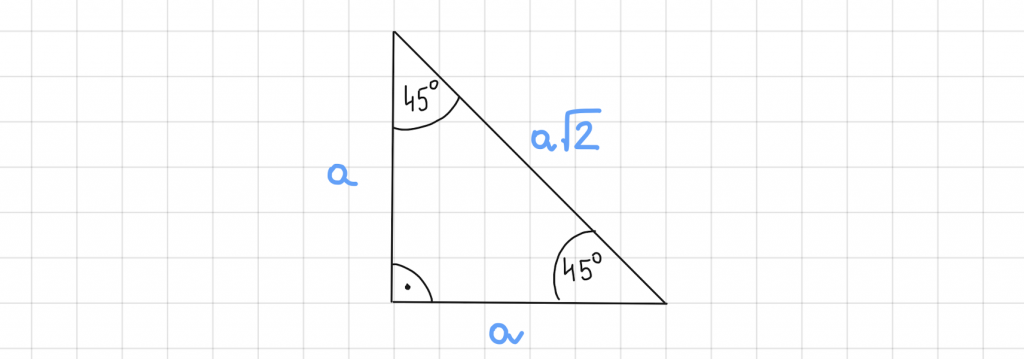
W ten sposób szybko można pozyskać niezbędną daną.
b) 30, 60 i 90 stopni
Trójkąt prostokątny o powyższych miarach kątów jest połową trójkąta równobocznego o boku oznaczonym jako „2a”. Bok, stanowiący przyprostokątną naprzeciw kąta 60°, można łatwo obliczyć z prostego wzoru:
a√3
Ponadto przyprostokątna, leżąca naprzeciw kąta 30°, równa jest połowie długości przeciwprostokątnej, czyli połowa wartości „2a”, to po prostu a .
Zwróćcie uwagę także na to, że w trójkątach o kątach 90°, 45°, 45° oraz 90°, 60°, 30° wystarczy znać długość jednego boku, aby obliczyć długość dwóch pozostałych. Wówczas dokończenie zadania nie powinno już stanowić dla Was problemu.
Wzory matematyczne, które warto zapamiętać
Jak widzicie, karta wzorów nie zagwarantuje Wam pełnego sukcesu. Choć obfituje w podpowiedzi, które mogą Was uratować w chwili kryzysu, nie należy opierać się wyłącznie na niej. Podczas powtórek starajcie się jak najwięcej materiału zrozumieć (zamiast wkuwania na pamięć), aby później bez trudu rozwiązywać zadania na egzaminie maturalnym.
Pozdrawiamy i życzymy dużo powodzenia na maturze! 🙂
Zespół Studniówki Maturalnej
Sprawdź szybkie i przyjemne przygotowanie do matury 2025
Dołącz do naszej platformy, a my zamienimy Twoje powtórzenie do matury w grę! Wszystko czego potrzebujesz podane na tacy ✅
